How to Overcome the Challenges of Error Correction in Quantum Computing
Are you struggling to navigate the complex world of error correction in quantum computing? Look no further! This article will guide you through the challenges and provide effective techniques to overcome them.
We’ll explore the background of quantum computing, delve into understanding quantum errors, and discuss innovative approaches to error correction.
By the end, you’ll be equipped with the knowledge to tackle error correction head-on and pave the way for a future of flawless quantum computing.
Key Takeaways
- Error correction techniques are crucial for ensuring the reliability and accuracy of quantum computations.
- Current error correction techniques have limitations in reducing errors and scalability due to high overhead and trade-offs between error reduction and computational resources.
- Advancements in error correction involve exploring new algorithms, including machine learning techniques and alternative methods like topological codes.
- Scaling error correction in quantum computing poses significant challenges due to increased sensitivity to errors, complex hardware requirements, and the need for optimized algorithms.
Background on Quantum Computing
Before diving into the challenges of error correction in quantum computing, it’s important to understand the background of quantum computing.
Quantum computing harnesses the principles of quantum mechanics to process information in a fundamentally different way than classical computing. This new paradigm holds great promise for solving complex problems that are beyond the reach of classical computers.
However, quantum computers are extremely sensitive to errors caused by quantum error sources, such as noise and decoherence. These errors can arise from factors like temperature fluctuations and electromagnetic interference.
To address these challenges, researchers have developed error mitigation techniques. These techniques aim to minimize the impact of errors on quantum computations by using error-correcting codes and error detection methods.
Understanding Quantum Errors
Once you grasp the concept of quantum errors, you’ll find it easier to navigate the complexities of error correction in this emerging field. Understanding error rates and error models is crucial in developing effective strategies for error correction in quantum computing.
To help you enjoy this topic, here are two sub-lists:
- Understanding error rates:
- Error rates refer to the probability of errors occurring during quantum operations.
- These rates vary depending on the specific quantum system and the quality of its components.
- Understanding error models:
- Error models describe the types of errors that can occur in a quantum system.
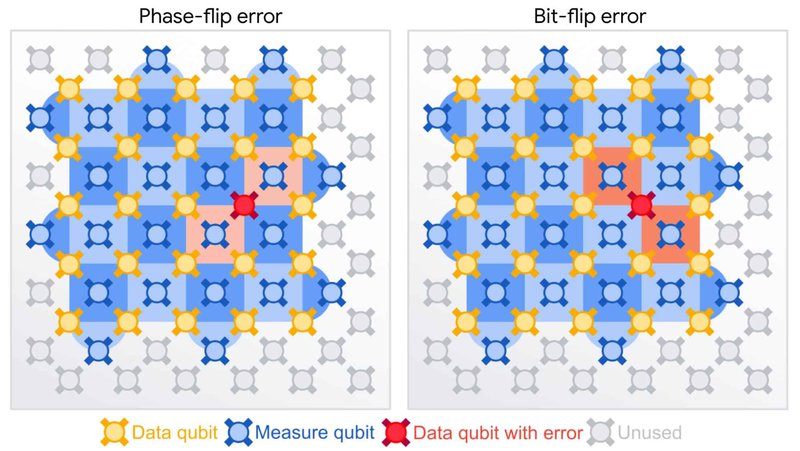
- Common error models include depolarizing noise, bit-flip, and phase-flip errors.
Techniques for Quantum Error Correction
In this discussion, we will explore the key points surrounding common error correction methods in quantum computing.
You will learn about the limitations of current techniques and understand the need for future advancements in error correction.
It’s important to understand these concepts as error correction plays a crucial role in ensuring the reliability and accuracy of quantum computations.
Common Error Correction Methods
There’s a variety of common error correction methods used in quantum computing. To help you understand these methods better, here are two sub-lists:
- Error Correction Algorithms:
- Shor’s algorithm: This algorithm is used for error correction in quantum computers and is based on the concept of quantum error correction codes.
- Steane code: It is a well-known error correction code that corrects errors caused by noise in quantum systems. It uses a combination of qubits and stabilizer measurements to detect and correct errors.
- Quantum Error Correction Codes:
- Surface code: This code is a promising approach to error correction in quantum computers. It uses a two-dimensional lattice of qubits to detect and correct errors.
- Stabilizer codes: These codes are a family of quantum error correction codes that can detect and correct errors by measuring stabilizer operators.
Understanding these common error correction methods is essential in building robust and reliable quantum computers.
Limitations of Current Techniques
Despite the progress made, current techniques for error correction in quantum systems still have limitations. While these techniques have shown promising results in reducing errors, they are not without their drawbacks. One limitation is the high overhead required for error correction, which can significantly limit the scalability of quantum systems. Additionally, the error correction process itself introduces its own errors, leading to a trade-off between error reduction and increased computational resources. Another limitation is the reliance on physical qubits for error correction, which are prone to their own errors and decoherence. To overcome these limitations, potential improvements can be explored. These include developing more efficient error correction algorithms, finding ways to reduce the overhead associated with error correction, and investigating alternative error mitigation techniques such as error-detecting codes or error-avoiding codes. By addressing these limitations, we can move closer to achieving fault-tolerant quantum computing.
| Limitations of Current Techniques | Potential Improvements |
|---|---|
| High overhead for error correction | Develop more efficient algorithms |
| Error introduction during correction | Reduce overhead associated |
| Reliance on physical qubits | Investigate alternative techniques |
Future Advancements in Error Correction
To advance error correction techniques, you can explore new algorithms, investigate alternative methods, and reduce the reliance on physical qubits. By doing so, you can pave the way for future advancements in error correction in quantum computing.
Here are some ways you can contribute to these advancements:
- Explore new algorithms:
- Implement machine learning algorithms to improve error correction.
- Develop algorithms that can handle larger numbers of qubits.
- Investigate alternative methods:
- Explore the use of topological codes for error correction.
- Investigate the potential of measurement-based error correction techniques.
Challenges in Scaling Quantum Error Correction
Scaling quantum error correction poses significant challenges in the field of quantum computing. As we strive to build larger and more complex quantum systems, the need for effective error correction becomes crucial. However, implementing error correction at scale is not an easy task. There are several challenges that researchers and engineers face in this process.
One of the main challenges is the scalability of error correction. Quantum systems are extremely sensitive to noise and errors, and as the number of qubits increases, so does the complexity of error correction. This leads to a higher probability of errors and a need for more intricate error correction codes.
Another challenge is the implementation difficulties of quantum error correction. The hardware required to perform error correction is complex and expensive. Additionally, the algorithms and protocols used for error correction need to be carefully designed and optimized for specific quantum systems.
To give you a better understanding of the challenges in scaling quantum error correction, let’s take a look at the table below:
| Challenges in Scaling Quantum Error Correction | Quantum Error Correction Implementation Difficulties |
|---|---|
| Increasing complexity of error correction codes | Complex and expensive hardware |
| Higher probability of errors | Careful design and optimization of algorithms |
| Need for more intricate error correction algorithms | |
These challenges highlight the need for ongoing research and development in error correction to enable the scalability of quantum computing systems. By addressing these challenges, we can pave the way for more reliable and robust quantum computers in the future.
Novel Approaches to Error Correction in Quantum Computing
In this discussion, you will explore novel approaches to error correction in quantum computing. We will focus on three key points: machine learning techniques, fault-tolerant quantum codes, and topological quantum error correction.
Machine learning techniques can be applied to improve error correction algorithms and optimize the performance of quantum systems. By using machine learning, we can train algorithms to better identify and correct errors in quantum computations. This can lead to more efficient and accurate error correction methods, ultimately improving the overall reliability of quantum computers.
Fault-tolerant quantum codes are essential for protecting quantum information against errors. These codes are designed to detect and correct errors that occur during quantum computations. By implementing fault-tolerant quantum codes, we can ensure that quantum information remains intact and reliable, even in the presence of noise and other sources of errors.
Topological quantum error correction utilizes the unique properties of topological systems to create robust qubits that are resistant to noise and errors. Topological systems are characterized by their ability to store and manipulate quantum information in a way that is highly resistant to environmental disturbances. By harnessing these properties, we can develop qubits that are more resilient to errors, making them ideal for use in quantum computing.
Machine Learning Techniques
Have you considered using machine learning techniques to address the challenges of error correction in quantum computing? Machine learning, specifically reinforcement learning, has shown promise in improving error correction algorithms by enabling systems to learn from their own experiences and make better decisions.
By pretraining models on large datasets generated from simulated quantum circuits, researchers have been able to improve the accuracy and efficiency of error correction algorithms. Additionally, data preprocessing techniques such as feature selection and dimensionality reduction have been used to enhance the performance of machine learning models in error correction tasks.
This combination of reinforcement learning and data preprocessing can greatly improve the error correction capabilities of quantum computing systems, paving the way for more reliable and scalable quantum technologies.
Benefits of using machine learning techniques for error correction in quantum computing:
- Improved accuracy and efficiency of error correction algorithms
- Ability to learn from experiences and make better decisions
Techniques used in machine learning for error correction in quantum computing:
- Reinforcement learning for training models on large datasets
- Data preprocessing techniques like feature selection and dimensionality reduction
Fault-Tolerant Quantum Codes
You can explore fault-tolerant quantum codes as a way to enhance the reliability and stability of quantum systems. One approach is to use fault-tolerant quantum gates, which are designed to withstand errors and maintain the integrity of qubits. These gates are essential for performing complex quantum computations accurately.
Another important concept in fault-tolerant quantum codes is the surface code. It is a two-dimensional lattice of qubits that allows for error detection and correction. The surface code can identify and fix errors through a process known as syndrome measurement, which involves measuring the state of multiple qubits.
Topological Quantum Error Correction
By implementing topological quantum error correction, you can enhance the reliability of quantum systems. This approach involves encoding quantum information in such a way that errors can be detected and corrected.
Here are some key points to help you understand topological error correction:
- Error detection: Topological codes can detect errors by looking for patterns in the physical qubit layout. These patterns, known as topological defects, are robust against noise and can be used to identify and locate errors.
- Example: You can think of these topological defects as knots or twists in the fabric of spacetime, which can be detected even in the presence of disturbances.
- Error correction: Once errors are detected, topological codes use a combination of quantum operations to correct them. This involves manipulating the physical qubits in a way that preserves the encoded quantum information.
- Example: Imagine untangling the knots in the fabric of spacetime to eliminate the errors and restore the correct quantum state.
Future Implications and Applications of Error Correction in Quantum Computing
There’s no doubt that the future implications and applications of error correction in quantum computing are fascinating and hold immense potential.
The potential applications of error correction in quantum computing are far-reaching, with the ability to impact various industries. The impact on industries could be revolutionary, as quantum computers could solve complex problems that are currently beyond the capabilities of classical computers.
For example, in the pharmaceutical industry, quantum computing could accelerate the process of drug discovery by simulating the behavior of molecules and predicting their properties.
In the financial sector, quantum computers could revolutionize cryptography, making data encryption more secure.
Additionally, quantum computing could greatly enhance optimization in logistics and supply chain management, leading to more efficient operations and cost savings.
The possibilities are endless, and the future of error correction in quantum computing is truly exciting.
Frequently Asked Questions
Are There Any Limitations or Drawbacks to Quantum Error Correction Techniques?
There are indeed limitations and drawbacks to quantum error correction techniques. While they offer promising solutions, challenges such as qubit decoherence and resource requirements must be addressed for effective error correction in quantum computing.
How Do Quantum Error Correction Codes Protect Against Different Types of Errors?
Quantum error correction codes protect against various errors by encoding information in a way that makes it resilient to disturbances. This has advantages in improving the stability and accuracy of quantum computing applications.
Can Quantum Error Correction Be Used to Correct Errors in Classical Computing as Well?
Yes, quantum error correction can potentially be used to correct errors in classical computing as well. It offers advantages over classical error correction techniques, such as the ability to correct for more complex errors.
What Are the Potential Risks or Challenges Associated With Implementing Error Correction in Large-Scale Quantum Systems?
Implementing error correction in large-scale quantum systems presents implementation challenges and potential risks. These include the complexity of designing and maintaining error correction codes, as well as the susceptibility to external noise and decoherence.
Are There Any Alternative Approaches to Quantum Error Correction That Are Being Explored?
There are alternative approaches to quantum error correction that researchers are exploring. These alternative approaches may offer future developments in overcoming the challenges of error correction in quantum computing.